I Global Circulation Model (GCM) sono quei modelli attraverso i quali i climatologi, in special modo i sostenitori dell’AGW, cercano di prevedere il clima della Terra anche a parechie decine di anni di distanza dal presente.

Vorrei spiegarvi alcuno dei motivi del mio scetticismo in merito.

Innanzi tutto, perdonatemi una premessa di tipo matematico, che segue il discorso iniziato nel post sulla interpolazione lineare ( http://daltonsminima.wordpress.com/2010/01/19/la-rubrica-di-nia-alcune-basi-statistiche-per-studiare-un-clima/#comments )

Riporto, l’estratto da wikipedia sull’interpolazione polinomiale

L’interpolazione polinomiale costituisce un’alternativa dell’interpolazione lineare: mentre per questo metodo si usa una sequenza di funzioni lineari si tratta ora di servirsi di un polinomio di un opportuno grado più alto.

Di una funzione f che in altra sede è nota si supponga di conoscere alcuni valori; in particolare si considerino i seguenti valori tabulati

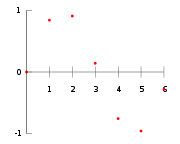
Diagramma dei punti dati.

x	f(x)
0	0
1	0.8415
2	0.9093
3	0.1411
4	-0.7568
5	-0.9589
6	-0.2794

Ci si chiede, per esempio: quanto vale la funzione in x = 2.5? L’interpolazione risolve problemi come questo.

Il seguente polinomio di sesto grado passa attraverso tutti i sette punti dati:

f(x) = – 0.0001521x⁶ – 0.003130x⁵ + 0.07321x⁴ – 0.3577x³ + 0.2255x² + 0.9038x.

Sostituendo x = 2.5, troviamo che f(2.5) = 0.5965.

In generale, se abbiamo n punti dati, esiste esattamente un polinomio di grado n-1 che passa attraverso tutti i punti dati.

Fin qui l’estratto da wikipedia.

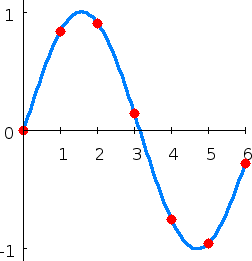
I lettori con qualche conoscenza di matematica avranno già riconosciuto che c’è un’altra funzione, che, più elegantemente, include i punti del diagramma, ed è la sinusoide, sen(x), un grafico che ha la forma di un’onda.

La f(x) e la sinusoide si assomigliano molto SOLTANTO nell’insieme considerato, cioè per x compreso tra 0 e 6 (quasi 6,28, un ciclo intero di 2p). In effetti, l’esempio di wikipedia ci fa vedere come fa (o potrebbero fare) una macchinetta calcolatrice a calcolare con buona approssimazione i valori di una funzione trigonometrica, o comunque periodica. Però fuori dall’insieme considerato, la f(x) e la sinusoide divergono completamente. Più ci si allontana dall’insieme considerato per l’interpolazione, più aumentano le probabilità che le due funzioni differiscano. Ad esempio per x= 9,42 (cioè 3p) abbiamo che:

sen(9,42) = 0 f(9,42) = -32,452

In sostanza, se l’interpolazione funziona, non è detto che funzioni anche l’estrapolazione.

Immaginiamo ora che il diagramma dei punti si riferisca a dati sperimentali di due grandezze fisiche, X e Y, cioè nella colonna a destra abbiamo i dati sperimentali dei valori assunti dalla grandezza Y al variare di X.

Utilizzando l’interpolazione, potremmo ipotizzare che la polinomiale f(x) sia la legge che interpreta il fenomeno fisico che lega le due grandezze, cioè Y=f(x). Tuttavia, senza un fase sperimentale a posteriori (cioè fuori dal range utilizzato per costruire l’ipotesi) non potremmo validare tale ipotesi. Magari la legge corretta, cioè quella più efficace nel prevedere i valori di Y, è Y=sen(x). In tal caso solo un’ulteriore verifica sperimentale, fuori dal range, ci farà capire che il modello Y=f(x) è sbagliato.

Conclusa la premessa, affrontiamo il tema dei modelli di tipo GCM utilizzati per prevedere l’evoluzione del clima.

Da quanto ho avuto modo di apprendere, tale modelli sono estremamente complessi e si basano sul tentativo di prevedere l’evoluzione del clima in base a leggi fisiche che determinano le principali grandezze climatiche (temperatura, umidità,ecc.) da un punto di vista statistico, su un periodo venti/trentennale. Naturalmente tutto è suddiviso per la varie zone del pianeta. Sono implementati, e di volta in volta raffinati, tenendo presente i dati climatologici disponibili, a partire grosso modo dal 1900, oltre ai dati paleoclimatici ottenuti con varie tecniche. In genere, propongono diversi scenari, a secondo dei valori assunti da varabili esogene.

L’idea di fondo è:

beh, se sono riuscito ad implementare un modello che si correla bene, o abbastanza bene, con un intero secolo, allora saprò farlo evolvere in maniera abbastanza corretta per prevedere statisticamente il futuro climatico.

Non sembra una cattiva idea, no?

Ora dimentichiamo per un attimo climategate, problema coi dati proxy, ipotesi di cherry-picking e via dicendo. Mettiamoci nell’ottica che coloro i quali hanno costruito i modelli siano programmatori, statistici, ricercatori in gamba e in buona fede.

Perché la cosa non dovrebbe funzionare?

Per rispondere, vediamo intanto come vengono raffinati i modelli. Laddove si nota uno scostamento tra quanto dice il modello e la realtà, quello che si fa, in genere, è cercare di capirne le cause, verificando se sia il caso di introdurre nel modello un nuovo fenomeno fisico-atmosferico se sia il caso di variare qualche parametro. Pare ragionevole. Se una volta inserito il nuovo fenomeno, il modello combacia meglio con il set di dati noto al ricercatore, verrebbe da dire che il modello è stato migliorato.

Ora, vediamo che significa fare questa operazione andando per analogia (sottolineo che è un’analogia non un confronto) con l’interpolazione polinomiale. Diciamo che la sinusoide è la legge fisica reale che lega le grandezze e la f(x) in un certo senso è il modello (è ovviamente un’iper-semplificazione, i modelli GCM sono effettivamente molto complicati). Immaginiamo che aumentando di poco il range di osservazione, mi sia accorto di uno scostamento tra la realtà e la f(x). Allora, cerco di capire il valore della realtà e prendo in considerazione un altro paio di punti ottenuti per via sperimentale, il 7 e l’8. Ricalcolo la f(x) ed ottengo una polinomiale di grado più alto (pari ad 8), cioè ho inserito nuovi parametri. A questo punto la mia f(x) assomiglia ancora di più alla realtà che conosco per certo, giacchè ho esteso il range da O-6 a O-8. Ma è migliorata da un punto di visto predittivo, cioè, è efficace nel prevedere i valori molto fuori dal range?

No, la funzione (il modello) continua a divergere completamente dalla realtà (la sinusoide) fuori dal range O-8, in particolare se si va molto fuori.

In sostanza, aumentare il numero di parametri per far aderire meglio il modello al set di dati noto al ricercatore non può servire per validare il modello stesso, nel senso che continuiamo a non conoscere la sua reale efficacia. Detto in altri termini, per validare qualsiasi legge fisica, o modello, serve la fase sperimentale. Mi rendo conto che può sembrare una banalità, eppure è utile ribadirlo.

Se un modello riesce a descrivere in maniera soddisfacente la realtà per il secolo passato, dove mai potrebbe essere l’errore?

Ad esempio, se non considerasse tutti i principali fenomeni fisici che influenzano il clima. In questo caso la correlazione con le grandezze prognostiche sarebbe ottenuta forzando i parametri che costituiscono i modelli per ottenere la correlazione cercata. A questo punto, il modello funziona solo se il fenomeno fisico ignorato rimane costante durante il periodo che viene considerato per la fase predittiva. Però, il modello non è più predittivo, cioè non risponde più alla domanda “COSA SUCCEDERA’?“, ma alla domanda “SE TUTTO CIO’ CHE IGNORO VA AVANTI COSI’, COSA SUCCEDERA’?”. In sostanza, il modello può essere utilizzato solo per fare proiezioni (projections), da non confondere con le previsioni (predictions).

Applichiamo queste considerazioni nella realtà dei GCM. Ipotizziamo che il clima dipenda dall’attività geomagnetica (come effettivamente credo) e che il modello non prenda in considerazione tale fenomeno, allora il modello potrà funzionare solo se il trend dell’indice si mantiene costante. Ma se l’indice cambia trend, ad esempio anziché continuare ad aumentare prende a diminuire velocemente, il modello, com’è ovvio, non funziona più. Il fatto che esso abbia prodotto risultati aderenti alla realtà già riscontrata in passato, non è una prova che abbia considerato tutti i fenomeni, specialmente se vi sono inclusi parecchi parametri sottoposti a tuning.

Tutto ciò, non è nemmeno una prova che i GCM non funzionino (forse prendono davvero in considerazione tutti i principali fenomeni che determinano il clima). E’ solo un ragionamento che giustifica un certo scetticismo su tali modelli.

Ma allora cosa si può fare per validare un modello?

La cosa più semplice sarebbe confrontarlo con la realtà successiva rispetto alla definizione del modello. Purtroppo, nei casi dei modelli GCM non si può fare, per lo meno breve. Il modello GCM si propone di individuare grandezze statistiche nell’arco di un trentennio (circa). Quindi, bisogno aspettare (almeno) trent’anni per potere verificare la bontà del modello. Tra l’altro, un periodo di trenta anni come tempo necessario per la verifica dei risultati, rende breve persino un periodo si cento anni come base per il modello.

In sostanza, al GCM, quali che siano i risusltati non si potrà mai dire:

“Guarda che negli ultimi dieci anni non ci hai azzeccato…”

Perché la risposta sarà

“E no! Devi aspettare trent’anni per giudicare”

A parte al fatto che durante i trent’anni il modello viene ulteriormente rivisto, è chiaro che nessuno ha tanto tempo da aspettare per validare il modello.

Ebbene, è evidente che se una teoria o un modello è costruito in maniera tale che, quale che siano i risultati, non si possa metterla in discussione, qualche problema c’è.

Su questo punto, però, lascio la parola agli epistemologi.

Agrimensore g.