ANNA MARIA LOMBARDI*, ALESSANDRO MANARA**
* Università di Padova, ** Osservatorio Astronomico di Brera

Sin dall’antichità sono testimoniate ricerche sui rapporti semplici che si ottengono mettendo in relazione tra loro le distanze e i moti medi dei pianeti. In questo lavoro, dopo aver presentato una breve rassegna dei modelli che dall’antichità fino a Keplero tentavano di scorgere in questa regolarità l’armonia del cosmo, prendiamo in considerazione modelli più recenti, in cui il ritrovamento di semplici frazioni è considerato utile per la comprensione del meccanismo di formazione del Sistema Solare. In particolare la nostra analisi si sofferma su un lavoro di Percival Lowell, per concludersi con una breve panoramica sulle ricerche contemporanee in questo settore.
Introduzione
La ricerca di regolarità tra i parametri dei fenomeni naturali è senz’altro una delle caratteristiche fondamentali del fare scienza dei periodi storici più diversi. Il nostro lavoro si propone di esaminare un ambito scientifico ben determinato, relativo ai tentativi di evidenziare l’esistenza di rapporti semplici tra i raggi delle orbite dei pianeti e/o tra i loro periodi. I modelli sono stati raggruppati in quattro paragrafi, rispettivamente relativi ai sistemi pre-copernicani, al significato di armonia nei modelli di Copernico e Keplero, alle ricerche di Lowell, e infine ai risultati e ai dibattiti più recenti. È stato così possibile riflettere da un lato sui comuni denominatori, dall’altro sulle differenze esistenti in contesti storici tra loro lontani, come pure sulle modalità con cui le regolarità tra i parametri vengono rintracciate, e sulle implicazioni da esse dedotte. Come prima osservazione, viene evidenziato come nel quadro precopernicano i raggi orbitali dei pianeti non erano misurati, bensì dedotti con l’ausilio di ipotesi a priori, tra cui spesso la convinzione che dovessero sussistere delle relazioni armoniche (cioè dei rapporti semplici, corrispondenti a intervalli musicali consonanti). Al contrario, in seguito la commensurabilità tra le orbite o tra i periodi dei pianeti viene ricercata a partire dalle misure sperimentali; l’abilità del ricercatore consiste allora nel far emergere le regolarità ipotizzate, ovvero nello scrivere l’effetto finale (non perfettamente regolare) come somma di più contributi, i quali individualmente presentano delle regolarità.
Anche il significato attribuito al rinvenimento di una commensurabilità nei parametri celesti muta nei diversi contesti. Se fino a Keplero una regolarità tra parametri naturali sottende una armonia progettuale divina, in seguito essa manifesta la presenza di forze ancora da individuare; effetti gravitazionali, dovuti a un pianeta ancora da scoprire; oppure conseguenze della particolare storia del nostro sistema solare.
Gli antichi
In questo paragrafo forniremo una rassegna di modelli astronomici in cui l’Armonia, intesa come concordanza musicale espressa da regolarità matematiche, è elemento chiave. A partire dalle testimonianze più antiche considereremo vari sistemi pre-copernicani, i quali privilegeranno come parametri di volta in volta le distanze dei pianeti dal centro del cosmo, piuttosto che la loro velocità angolare o le posizioni relative da essi assunte. In particolare evidenzieremo gli sforzi volti a sostituire valori dedotti da ipotesi a priori (per esempio la stessa esistenza di Armonia dei cieli) con risultati ottenuti da misure indirette.
Le prime informazioni sui valori attribuiti alle distanze dei pianeti dalla Terra risalgono al VI secolo a.C. fu Aristotele (nel IV secolo) a stendere per primo un resoconto dei modelli degli antichi, anche se le informazioni che sembrano risalire più addietro ci arrivano da Simplicio, che scrive nel II secolo d.C. e la cui testimonianza dobbiamo quindi considerare con una certa cautela. È questa la fonte che ci informa sul sistema utilizzato da Anassimandro, in cui i pianeti, non distinti dalle altre stelle, si trovano a una distanza dalla Terra che è pari a 9 volte il raggio della Terra, la Luna a 18, il Sole a 27.
È poi possibile confrontare diverse fonti a riguardo del modello costruito da Pitagora e in seguito adottato dai suoi seguaci, in quanto esso viene descritto per esempio da Plinio il vecchio, da Marziano Capella e da Censorino. I Pitagorici avrebbero cercato di ricavare le distanze dei pianeti dall’ipotesi che esse dovessero
manifestare proporzioni armoniche, ovvero proprio quei rapporti numerici semplici che si era scoperto caratterizzare gli intervalli musicali fondamentali (2:1, 3:2, 4:3). Attraverso questi rapporti essi arrivarono a individuare il rapporto che caratterizzava le due unità fondamentali per la costruzione della scala musicale, il tono e il semitono: ecco che il Sistema Solare nelle sue distanze presentava le stesse proporzioni di una scala musicale! Secondo le testimonianze dei suddetti storici, l’unità fondamentale di misura, pari a 126.000 stadi, sarebbe stata ricavata da calcoli e misure, anche se non viene rivelato come. Molti furono coloro che si richiamarono in seguito al sistema pitagorico, tra cui Teone, Achille Petavio e altri. Il primo modello che possiamo conoscere da fonte diretta è quello platonico, risalente al IV secolo a.C. per fissare le distanze dei pianeti dalla Terra, Platone considerò le prime due serie geometriche: 1, 2, 4, 8 e 1, 3, 9, 27. Ordinandole ottenne una successione di distanze (relative) per cui, se la Luna dista 1 dalla Terra, il Sole dista 2, Venere 3, Mercurio 4, Marte 8, Giove 9, Saturno 27. Platone stesso sottolinea come (escludendo il 27) si tratti degli stessi numeri che caratterizzano gli intervalli musicali consonanti.
Di pochi anni successivo è il sistema di Eudosso di Cnido, che introduce però una grossa novità: la proporzione che egli presenta tra le distanze Terra-Luna e Terra-Sole (pari a 1:9, ovvero al rapporto esistente tra un tono e la sua quinta, come osserva l’astronomo greco) viene ricavata dall’osservazione delle eclissi supportata da un ragionamento geometrico, e non presupposto a priori. La prima misurazione della distanza Terra-Luna nota risaliva ad Aristarco (II sec. a.C.); essa era una misura relativa – Luna-Terra in rapporto a Terra-Sole – e sfruttava la posizione di Luna perfettamente semipiena (era stato dedotto un rapporto di 1:19, mentre oggi sappiamo che tale rapporto è inferiore a 1:400). Eudosso riuscì a trasformare il dato relativo in assoluto, sfruttando una eclissi lunare di massima durata2. In seguito il modello di Eudosso venne mal interpretato (per esempio da Plinio) partendo dal fatto che le distanze dovevano formare un intervallo di quinta, e attribuendo quindi a loro una valore relativo di 3:2.
Sottolineiamo come fino a questo momento nei diversi modelli si trova sempre che la Luna, considerato allora come il pianeta più interno, è associato alla nota più grave (un altro esempio famoso si trova anche in Cicerone); questa interpretazione deriva dall’osservazione che corpi in moto più lento producono suoni più gravi. In seguito a questi si affiancano sistemi in cui il pianeta più interno, a una distanza minore, è associato alla nota più acuta, come se la distanza del pianeta dal centro del cosmo fosse proporzionale alla lunghezza di una ideale corda sonora, che tanto più corta produce un suono più acuto. Si tratta di un modello in cui le distanze sono poste in diretta analogia con le lunghezze delle corde di una astratta lira greca, il quale, esplicitato tra i primi da Nicomaco Neo-pitagorico, si troverà ancora nei trattati di astronomia e di teoria musicale del XVI secolo. Molto simile a questo sono i modelli in cui il Sistema Solare è messo in analogia con un monocordo; in quel caso (di cui famoso esempio è il Monocordo del Mondo presentato da Robert Fludd nel suo Utriusque Cosmi) non abbiamo un set di più corde, ma un’unica corda sulla quale i pianeti sono posizionati come ideali capotasti. L’armonia musicale viene cercata non solo utilizzando i raggi delle orbite dei pianeti, ma anche in altri parametri come per esempio in quelli tipici degli aspetti, quelle particolari posizioni reciproche degli astri che assumevano un ruolo fondamentale in astrologia. Proprio il rintracciare armonia in queste disposizioni celesti sembrava giustificare il fatto che in quelle precise posizioni gli astri influissero sull’animo e sul carattere dell’uomo: il fatto che esistano dei rapporti armonici tra gli astri spiega perché noi «risuoniamo», siamo «in risonanza» con particolari configurazioni celesti. In pratica in quel caso la nostra anima riconosce la stessa musica che poi apprezza sulla Terra quando è suonata da una voce o da uno strumento [Kassler 1982].
Per esempio Tolomeo nel II secolo d.C. studiava i rapporti tra gli angoli caratteristici dei diversi aspetti (opposizione, trigono, quartile, sestile), ricavandone quelle semplici frazioni che nella musica antica rappresentavano gli intervalli consonanti (vedi fig.1). Più sottile l’analisi di Nicola Oresme, lo studioso francese del XIV secolo. Egli rintracciava l’armonia nei lati dei poligoni tipici degli aspetti, anziché negli angoli corrispondenti. Ancora una volta si trovavano i rapporti caratteristici delle consonanze, ma questa volta i rapporti erano sotto radice quadrata (per esempio al posto di 3:2, rapporto che rappresenta una quinta, si trovava √3:2). Si trattava quindi di un’armonia «celata» da una radice, che la trasformava in un numero irrazionale. Proprio nella natura di questi numeri sembrava indicata l’inafferrabilità da parte dell’astrologia degli umani destini, così come era impossibile conoscere quei numeri in maniera esatta. A queste riflessioni egli dedicò il Tractatus de commensurabilitate vel incommensurabilitate motuum coeli.
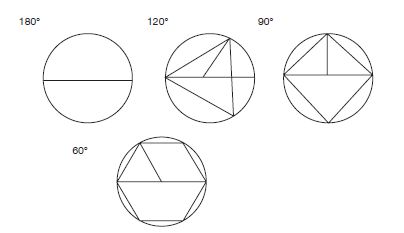 Fig. 1 Tolomeo mostra che gli angoli sottesi nelle configurazioni da sempre prese in considerazione
Fig. 1 Tolomeo mostra che gli angoli sottesi nelle configurazioni da sempre prese in considerazione
dall’astrologia (opposizione, trigono etc.) danno origine a rapporti corrispondenti
agli intervalli fondamentali della musica di quei tempi (ottava, quinta e quarta). Qui
le Armonie (intervalli musicali) si trovano nei rapporti tra gli angoli. Per esempio il rapporto
tra gli angoli al centro individuati da una retta e da un triangolo equilatero danno origine
a un intervallo sesquialtero, o di quinta: 180°:120° = 3:2.
 Fig. 2. Nel modello di Nicolas Oresme le Armonie (intervalli musicali) sono «celate» alla
Fig. 2. Nel modello di Nicolas Oresme le Armonie (intervalli musicali) sono «celate» alla
ragione dalla radice quadrata, ragione per cui l’Astrologia non può predire completamente
il futuro dell’individuo e del Mondo. Ad esempio il rapporto conosciuto come «medietas
sesquialtera» risulta essere: AC:AD = √3:2.
Riportiamo infine il sistema tramandato da Marziano Capella, il quale – rifacendosi a fonti romane risalenti al I secolo a.C. – attribuiva una proporzione diretta tra le distanze e i periodi dei pianeti. I rapporti tra le distanze sarebbero quindi gli stessi che si osservano tra i periodi, ovvero i seguenti:
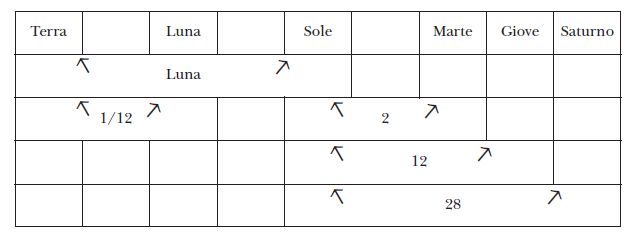 Si deve sottolineare che adottando il sistema tolemaico è impossibile dare una stima delle distanze planetarie, mentre è possibile fornire per ciascun pianeta il rapporto relativo tra epiciclo, deferente ed eccentrico.
Si deve sottolineare che adottando il sistema tolemaico è impossibile dare una stima delle distanze planetarie, mentre è possibile fornire per ciascun pianeta il rapporto relativo tra epiciclo, deferente ed eccentrico.
Una stima delle dimensioni dell’Universo e della distanza dei pianeti dalla Terra veniva fatta assumendo l’ipotesi del plenum, ovvero l’idea aristotelica che non potesse esistere uno spazio vuoto. Su questa asserzione era stato costruito un modello di universo come successione di sfere materiali, ciascuna della larghezza necessaria a contenere il moto non esattamente circolare di un pianeta. Ogni sfera aveva il
bordo interno di raggio pari alla minima distanza a cui quel dato pianeta poteva essere osservato, e il bordo esterno di raggio pari alla distanza massima, il suo spessore essendo definito dal diametro dell’epiciclo. Conoscendo – dalle misure di Aristarco – il valore delle distanze dalla Terra di Sole e Luna, e i valori relativi di deferenti ed eccentrici per i diversi pianeti, era possibile ottenere la misura delle dimensioni delle sfere planetarie, nonché dare una stima del raggio dell’Universo. Questo modo di calcolare le distanze è tipico in tutto il periodo compreso fra Tolomeo e Copernico. Grazie all’introduzione del sistema Copernicano è invece possibile realmente calcolare le distanze dei vari pianeti dal Sole.
Da Copernico a Keplero: l’armonia riscoperta, l’armonia misurata
Che l’attenzione ai risvolti «armonici», musicali in senso matematico, dei modelli astronomici sia ancora viva alle soglie della Rivoluzione scientifica è testimoniato dalle parole dello stesso Copernico, che nel De Revolutionibus sostiene come un grosso successo del proprio sistema il fatto che, se si considerano i periodi dei pianeti ordinati secondo la loro distanza dal Sole, si ritrova finalmente una successione monotona: «Troviamo dunque in questa disposizione una ammirevole simmetria del mondo e un rapporto armonico preciso tra movimento e grandezza delle sfere, quale non è possibile rinvenire in altro modo». Sono così poste le basi per rintracciare quella relazione tra distanze e periodi che era stata supposta sin dall’antichità, e che sarà formalizzata in quella che è nota come Terza legge di Keplero. In effetti l’astronomo tedesco dedicò molti anni alla ricerca di un’armonia celeste, dove il termine armonia è ancora inteso in senso tecnico, e strettamente connesso alla teoria musicale: per almeno 23 anni egli provò a determinare tra quali parametri del Sistema Solare esistessero dei semplici rapporti commensurabili. Questi non sarebbero dovuti essere casuali, ma coincidenti con quelle semplici frazioni che in quegli anni rappresentavano gli intervalli consonanti, ammessi dalla teoria musicale.
Nelle sue ricerche, iniziate già dai tempi del Mysterium Cosmographicum, e quindi dalla fine del XVI secolo, tentò di rintracciare tali rapporti dapprima tra le distanze dei pianeti dalla Terra o dal Sole, poi tra i moti medi, senza peraltro riscontrare un risultato armonico preciso. Eppure, se l’armonia delle sfere doveva rispecchiare l’armonia della creazione, non era possibile accontentarsi di una semplice approssimazione: perciò la ricerca dello scienziato tedesco non si arrestò, raggiungendo una precisione assai maggiore considerando non la velocità media dei pianeti, bensì le due velocità estreme dei singoli pianeti, quelle misurate all’afelio e al perielio di ciascuno. Nella tavola (traduzione di quella realizzata dallo stesso Keplero
nell’Harmonice Mundi) è possibile osservare i rapporti rintracciati, e a fianco l’intervallo musicale a essi relativo. I valori delle velocità si riferiscono alle velocità angolari all’afelio e al perielio.
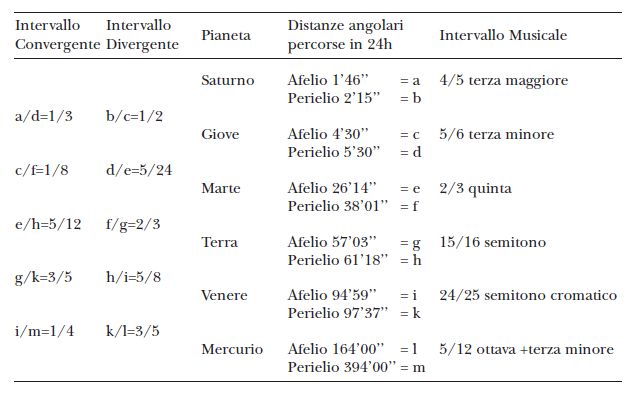 In seguito, il tentativo di rintracciare semplici frazioni, o relazioni numeriche ricorrenti, perde il carattere metafisico che apparteneva ai secoli precedenti, pur senza sminuire l’importanza di questo tipo di attività di ricerca. Lo scopo non è più quello di leggere nell’armonia l’impronta di un creatore, quanto quella di scorgere nelle regolarità dei parametri planetari la presenza di forze non ancora rivelate osservativamente. Senza la pretesa di esaminare in profondità le ricerche fatte lungo i secoli in questo ambito, citiamo come esempio significativo la legge di Titius-Bode, scoperta nel 1766 da Johann Titius e in seguito formulata matematicamente e divulgata da Johann Bode (1778). Essa fornisce per il semiasse maggiore a dell’orbita di un qualunque pianeta del Sistema Solare il valore:
In seguito, il tentativo di rintracciare semplici frazioni, o relazioni numeriche ricorrenti, perde il carattere metafisico che apparteneva ai secoli precedenti, pur senza sminuire l’importanza di questo tipo di attività di ricerca. Lo scopo non è più quello di leggere nell’armonia l’impronta di un creatore, quanto quella di scorgere nelle regolarità dei parametri planetari la presenza di forze non ancora rivelate osservativamente. Senza la pretesa di esaminare in profondità le ricerche fatte lungo i secoli in questo ambito, citiamo come esempio significativo la legge di Titius-Bode, scoperta nel 1766 da Johann Titius e in seguito formulata matematicamente e divulgata da Johann Bode (1778). Essa fornisce per il semiasse maggiore a dell’orbita di un qualunque pianeta del Sistema Solare il valore:
a = 0.4 + 0.3 x 2n
Come noto, la legge ebbe una risonanza clamorosa nel 1781, quando William Herschel scoprì il pianeta Urano proprio alla distanza prevista dalla legge.
Non sempre la regolarità può essere espressa in maniera semplice, e lo sforzo dello scienziato è allora rivolto a svelarla, scomponendo i contributi di più effetti. Se già Keplero adottava il concetto di composizione di forze per spiegare come una azione a simmetria sferica o circolare, come immaginava essere quella del Sole, potesse dare luogo a un’orbita ellittica (egli non immaginava che la forma ellittica potesse essere una soluzione per le forze proporzionali all’inverso del quadrato della distanza), con l’adozione della meccanica di Newton quello di riuscire a districare un fenomeno apparentemente complesso nella somma di più componenti semplici e simmetriche diviene uno sforzo diffuso, che ha il suo culmine nel successo dello sviluppo di Fourier. Il sistema solare diviene una palestra in cui dimostrare la grandezza dell’edificio fondato da Newton e ogni discrepanza diviene origine non di una crisi, bensì di una nuova ipotesi. Sarà così che Adams e Leverrier, con il metodo delle perturbazioni gravitazionali, consentiranno la scoperta di Nettuno, e che sull’impulso dato dalla teoria delle risonanze di Lowell, i suoi allievi scopriranno
Plutone. In realtà gli studi intrapresi da Lowell sono ai nostri occhi particolarmente interessanti, in quanto egli non si limitò a sfruttare una ipotesi di risonanza per individuare l’eventuale presenza di nuovi pianeti, ma la utilizzò per scegliere un modello di formazione del Sistema Solare. Come vedremo più avanti, questo tipo di analisi sarà poi proprio della ricerca del XX secolo, e in questo senso si può ammirare nell’astronomo americano un pioniere di questo ambito di studi.
Fine -1° parte-
siamo tutti in vacanza
io sono fino al 26 in montagna
per cui ci si rivede per il 27
ciao e buon Natale a tutti
FBO(Quote) (Reply)
Bello! Mi piace questo modo di vedere le cose…
Come ho sempre pensato la Natura ( N maiuscola… ) “ragiona” secondo leggi semplici e cerca sempre l’equilibrio col minor dispendio di energia….
Buon Natale a tutti !!!
Gianluigi(Quote) (Reply)
Il solito ..
😀
ci sono anche tante persone che lavorano in questi giorni.
@Gianluigi
Se sei un “fan” delle armonie che troviamo in natura, ti consiglio la lettura di questo mio articolo:
http://daltonsminima.altervista.org/?p=18827
Anche se questa prima parte potrà sembrare un pò pesante..per i contenuti storici, vi consiglio di pazientare..
La seconda è estremamente interessante in riferiemento alle ricerche dei nostri giorni.
Siamo sotto giorni di festa, ho deciso quindi di impostare una linea “editoriale”, leggera e sobria.
Michele(Quote) (Reply)
Vedi:
http://www.giurfa.com/unified_field.xlsx
Adolfo Giurfa(Quote) (Reply)
@Michele
Ricordo bene l’articolo che hai citato, affascinante!
Quante cose curiose e stupende ci sono in natura, non basterebbe una vita per conoscerle tutte.
Ma grazie a NIA una buona parte verra mostrata.
Ancora Buon Natale a tutti !
P.s.
Andate piano con lo spumante ( lo champagne ?… sciacquetta a confronto… ) che c’e’ ancora Capodanno…..
😉
Gianluigi(Quote) (Reply)