In un recente articolo postato da ice si parlava delle differenze tra il SN fornito da SIDC e quello ottenuto utilizzando il metodo di NIA. Le discrepanze sono visibili a colpo d’occhio, ovviamente. Quello che mi sono chiesto è se era possibile, in qualche modo, riuscire a stabilire oggettivamente la maggior validità di un metodo di conteggio rispetto ad un altro. Sono partito da questa idea: il SN dovrebbe essere un valore che sta a rappresentare l’effettiva attività solare del momento in cui si compie la misurazione del SN stesso. D’altra parte, anche i valori del SF sono, come tutti sappiamo, un indice dell’intensità di attività solare. Ora, il SF è un valore misurabile, è cioè oggettivo come una misura di temperatura, di peso eccetera. Il SN è invece una interpretazione dell’attività del sole, e diversi osservatori forniscono differenti interpretazioni, secondo le loro regole.
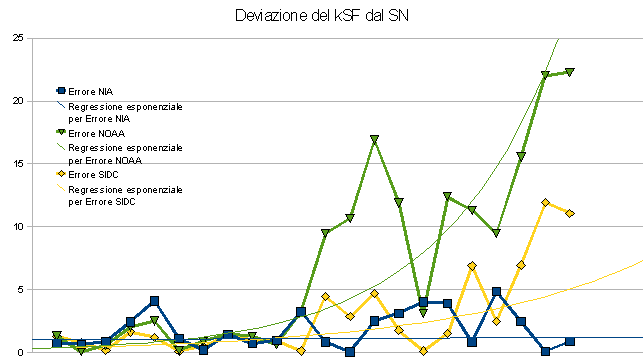
Il criterio che ho seguito per testare la validità di diversi conteggi (NIA, SIDC e NOAA) è il seguente: un buon conteggio deve essere una reale immagine dell’attività solare del momento, conseguentemente deve essere in relazione lineare (ovviamente con margine di errore) con il solar flux.. Ho quindi creato una tabella che raccogliesse i SN dei diversi conteggi e il SF a partire da gennaio 2009, e poi ci ho lavorato un po’:
La colonna kSF indica una lista di valori che sono ottenuti moltiplicando per un certo fattore costante (k) il SF e sottraendo al risultato un fattore fisso (i). Per ricavare k ed i ho proceduto per tentativi costruendo una funzione lineare che interpolasse bene i primi punti di ogni grafico dei conteggi. Questa colonna, in breve, è una previsione teorica del SN a partire dal SF, secondo una relazione matematica lineare. Le colonne degli errori sono date dal valore assoluto della differenza tra kSF e SN fornito dal conteggio preso in esame, e servono a verificare se il conteggio soddisfa la relazione lineare costruita o meno in un dato punto del grafico.
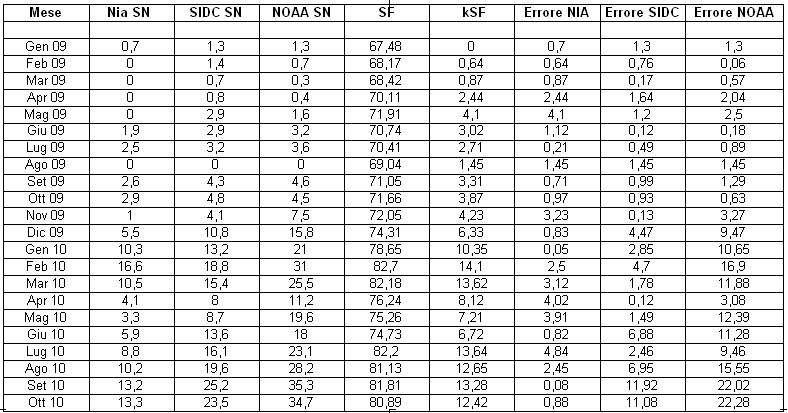
Siccome un immagine spesso vale più di mille parole (specie per i discorsi un po’ incasinati), ecco due grafici:
In rosso è rappresentato il SN previsto dal modello basato sul SF, gli altri colori indicano i SN effettivi forniti dai conteggi. Penso sia già abbastanza eloquente, ma andiamo più in là: il grafico che segue ha molto da dire:
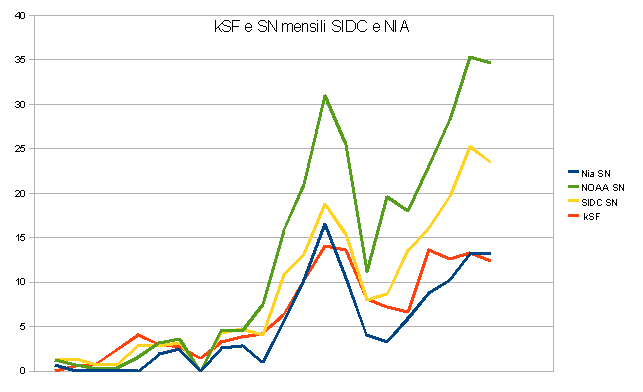
Questo è il grafico delle differenze tra SN previsto e SN effettivo dei conteggi. Per i primi punti tutti i grafici indicano che i conteggi soddisfano la relazione matematica. Ma solo il NIA’s count rimane sempre sotto un errore di 5 punti e, soprattutto, non tende a crescere (linea di interpolazione piatta, quella blu).
Tutto sto macello per dire che???
… per dire che il numero di macchie fornito dal metodo di conteggio di NIA è in relazione lineare con il solar flux, e precisamente, dopo tutta questa carta buttata via, possiamo dire che:
NIA’s SN = (SF x 0,9265) – 62,52
(ATTENZIONE! – FORMULA EMPIRICA – NESSUNA VALIDITA’ SCIENTIFICA – UTILIZZARE CON CAUTELA)
Cosa ce ne facciamo?
Non ne ho idea, che domande! 😀 Però mi è sembrata interessante come osservazione. Penso che sia una buona indicazione del fatto che il conteggio utilizzato da NIA è veramente un indice affidabile dell’attività solare.
Andrea
(e che gli venga un’accidente a quelli del NOAA, che non mi fanno entrare negli archivi dei SN mensili e me li sono dovuti fare come media dei giornalieri… Scusate eventuali errori nei valori)
Bravi ragazzi ma io non avevo dubbi andate avanti così e non guardiamo più in faccia a nessuno 🙂
andrew(Quote) (Reply)
Grande lavoro Andrea,complimenti per l’impegno e la passione.
Avanti con questo grande minimo!
Avanti così tutti quanti che siete grandi!!
enzor(Quote) (Reply)
Dai grafici di Svalgaard: Questo é il paragone tra il SF del minimo del 1954 con l´attuale:
http://www.leif.org/research/F107%20at%20Minima%201954%20and%202008.png
E questo che dimostra come la teoria di L&P sia ancora confermata con il calo della forza magnetica nel Sole:
http://www.leif.org/research/Livingston%20and%20Penn.png
Il bel lavoro di Andrea ci conferma che i SN di SIDC (un poco meno) e NOAA (MOlto) sono ormai fuori della realtá e che il SF e il NIA´s cont sono validi e coerenti con la teoria di L&P.
Bravo Andrea!
sand-rio(Quote) (Reply)
ci sarà un motivo se è sempre stato il punto focale su cui puntare.
Fabio Nintendo(Quote) (Reply)
Avete visto:
http://www.landscheidt.info/?q=node/50.
e:
http://www.vukcevic.talktalk.net/PF.gif
L’elettrocardiogramma del Sole, che porta a quella dell’Universo Elettrico
http://www.holoscience.com/
e, invero, il campo unificato:
http://www.scribd.com/doc/40514613/Unified-Field-Explained-8
Adolfo Giurfa(Quote) (Reply)
Grazie a tutti quanti per i complimenti! A questo punto, dato che l’argomento interessa, mi metterò un po’ a studiare anche il ciclo 23 per fare qualche calcolo un po’ più preciso… Arrivederci al prossimo aggiornamento!
Andrea311(Quote) (Reply)
@ Paola
Il tuo commento è stato “temporaneamente” eliminato!
L’amministratori sono stati molto chiari nei passati giorni:
http://daltonsminima.altervista.org/?p=12154#comment-34050
Michele(Quote) (Reply)
Mi viene in mente che questo lavoro potrebbe avere un peso in tutti quegli studi che inferiscono l’attività solare (anche) dall’SN. Il NIA’s count potrebbe metterli in discussione. Beh, forse mi sono spinto un po’ troppo oltre, però…
agrimensore g(Quote) (Reply)
@agrimensore g
Calma. Questa formula è un’idea, un’idea da verificare… Ci lavorerò! 🙂
Andrea311(Quote) (Reply)
http://daltonsminima.altervista.org/?p=9514&cpage=1#comments
sand-rio(Quote) (Reply)
Per gioco ho preso i dati della tabella e ho messo il tuto in un foglio excel. Ho poi fatto i grafici mettendo SF in ascissa e SN in ordinata, per tutti e tre i coonteggi (NIA, SIDC e NOAA). Poi mi sono fatto dare le linee di tendenza (lineari) con i relativi coefficienti di correlazione R^2:
NIA: SN* = 0.9142 SF – 63.048 R^2 = 0.8704
SIDC: SN* = 1.4088 SF – 96.035 R^2 = 0.8763
NOAA: SN* = 2.2178 SF -152.21 R^2 = 0.9001
Di conseguenza, da questi dati, risulta che il conteggio NOAA è il più affidabile (R^2 maggiore), quello NIA il meno affidabile. Provare per credere.
Cosa non va nell’articolo:
1- si è usata una sola linea di tendenza, riferita ai primi dati, che però sono abbastanza simili tra loro e quindi le differenze sono poco significative. Infatti quando poi i dati iniziano a differire la relazione trovata non li rappresenta bene.
2- evidentemente il SF non è legato in modo lineare al SN.
Aggiunta di una osservazione:
dal moemnto che il dato certo è il SF (misurato strumentalmente senza interpretazioni di sorta), la legge che si dovrebbe cercare non è a mio parere SN = SN(SF), bensì l’inversa, ovvero SF = SF(SN), che nei tre casi è (sempre ricavate con la linea di tendenza di excel):
NIA: SF* = 0.952 SN + 69.695 R^2 = 0.8704
SIDC: SF* = 0.622 SN + 68.963 R^2 = 0.8763
NOAA: SF* = 0.4058 SN + 69.228 R^2 = 0.9001
Questo perchè la relazione stima, in base al conteggio SN, il valore di SF*, da confrontare con quello effettivamente misurato SF.
Per ora ho pensato solo a questo.
edoardo(Quote) (Reply)
@Andrea311
Sì, naturalmente, era tanto per dire… Rispetto all’osservazione di edoardo, mi potresti spiegare meglio come hai calcolato k e i?
@Sand-rio
Ho visto la’rticolo (interessante) e i commenti postati, qualcuno mi trova proprio d’accordo. Ma temo andiamo un po’ OT.
agrimensore g(Quote) (Reply)
hai sbagliato approccio, non esiste correlazione lineare tra SN e SF, ne per i dati NIA, ne per il SIDC ne per il NOAA.
la correlazione esiste nella misura in cui si valuta l’andamento generale degli indici e si nota come SIDC e NOAA non seguono i rapporti di forza tra i valori di SF
Fabio Nintendo(Quote) (Reply)
@Fabio Nintendo
Perchè ho sbagliato approccio? Ho cercato una legge lineare, come proprotso nell’articolo, per ciascun tipo di conteggio, e ho trovato che il più fedele (se si ipotizza appunto una legge lineare) è quello NOAA. Non ho fatto altro che approfondire l’articolo.
edoardo(Quote) (Reply)
@edoardo
Spiegami cos’è il coefficiente r^2, che non ho ben inteso cosa vuoi dire. Ad ogni modo, rispondendo alle tue osservazioni:
1) le Linee di tendenza sono 3 e non una, ce n’è una relatiiva a ogni grafico degli errori dei conteggi. Quella degli errori NIA rimane piatta in relazione alla formula lineare.
2) Nel periodo preso in esame, il NIA’s count fornisce valori compatibili con un’approssimazione lineare (questo è un dato di fatto, sul resto si può discutere)
Detto questo, penso anch’io che la legge generale sia di natura leggermente esponenziale, ci si deve riguardare… al di la di tutto, comunque, NOTA CHE IL NIA’S COUNT FORNISCE UGUALI SN PER UGUALI SF (grafico 1), gli altri conteggi a parità di sf hanno aumentato il sn. Questo è un dato di fatto.
Dopodichè, continua pure a cercare delle falle perchè sicuramente ce ne sono a iosa! 😀
Andrea311(Quote) (Reply)
@Andrea311
il coefficiente R^2 è il coefficiente di regerssione, un indice della bontà della linea di tendenza. Più si avvicina all’unità, più la linea di tendenza rappresenta in modo corretto i dati.
Tu hai fatto le linee di tendenza degli errori, non degli andamenti. Di quelli hai solo la legge che hai trovato. Ora abbiamo due problemi:
1- tu hai tre set di dati indipendenti (fa niente che misurano la stessa quantità , sono stati ricavti indipendentemente l’uno dall’altro e con ipotesi di base diverse). Quindi devi avere tre leggi, una per set di dati. Non li puoi legare tra loro essendo indipendenti, altriemnti trovi una relazione “media”, che non significa nulla.
2- la legge che hai trovato è stata sviluppata sull’analisi dei soli dati iniziali, quelli dove i tre set dati differiscono per poco (il che significa anche che sono poco significativi, tra l’altro, per lo scopo che ti sei prefisso). Per questo motivo ti risulta una legge che si applica mediamente bene al NIA, perchè questo conteggio è “stabile” (=varia poco) al variare del SF. Perciò anche l’errore NIA è stabile , come dici tu. Esso però è riferito ad una legge non valida per gli latri due conteggi (SIDC e NOAA)..
edoardo(Quote) (Reply)
@agrimensore g
k e i sono coefficenti empirici, cioè sono venuti fuori da dei tentativi di costruire un valido fattore di conversione tra SF e SN rimanendo su una relazione lineare.
p.s NOTA: ho appena fatto qualche test preliminare sui valori del ciclo 23… è probabile che ci sia qualcosa da modificare soprattutto nel massimo del ciclo, ma molto meno di quello che mi aspettavo. Per la settimana prossima vedo di uscire con dei dati alla mano…
Andrea311(Quote) (Reply)
@edoardo
Ah, ok. Sono arrivato a capire cosa vuoi dire. Beh, mi fido! Certamente non ho verificato i coefficienti di correlazione lineare delle serie di dati, l’ho detto: ho fatto diverse prove e ho tirato fuori quella funzione lineare che mi sembrava la più corretta.
Detto questo, comunque, ripeto (per la centesima volta.. :D) è tutto da riguardare, perchè:
1) I dati sono riferiti ai valori mensili misurati e non a quelli smoothed (abbastanza rilevante)
2) Non è detto che la relazione sia strettamente lineare
3) Ho analizzato (alla bell’e meglio) 22 mesi di valori… Praticamente un niente
ERGO: grazie per la segnalazione, per l’analisi successiva riparto da qui!
Andrea311(Quote) (Reply)
@Andrea311
@edoardo
Questo é il bello di NIA: Siamo qui tutti per imparare e migliorare. Nessuno con la certezza di avere la veritá assoluta in tasca.
Complimenti a tutti!
sand-rio(Quote) (Reply)
intanto proprio adesso è andato in onda su tgr leonardo a rai 3 uno dei tanti servizi terroristici sul GW.
Hanno detto che, secondo le stime di un progetto europeo (non ho capito a quale progetto facessero riferimento), entro il 2100 scompariranno tra il 50 e il 90 % dei ghiacciai e la neve verrà sostituita dalla pioggia con tutte le conseguenze del caso
Maunder(Quote) (Reply)