Ne geocentrico, ne eliocentrico ma ……
– Premessa
A molti di voi questa storia potrà sembrare frutto di una mente che ama un pò troppo fantasticare e che nel corso della sua vita è sempre stata in cerca di relazioni o “far tornar i conti” a proprio piacimento. Una storia dai connotati più da programma televisivo alla Voyager, che più da blog che tratta tematiche scientifiche interne al nostro sistema solare. Ho tuttavia deciso di riportare questa storia, non tanto per le esperienze di stampo strettamente paranormale, ma per le straordinarie relazioni matematiche, che nel corso della sua vita, queste simpatico personaggio di Port Aransas in Texas (Usa), ha ricavato all’interno del nostro sistema solare.

– La storia
Alan Bennett (1936 – 2003) era un marinaio per vocazione la cui passione, o “raison d’etre“, era però rivolta all’astronomia, dopo che lui e un suo collega avevano vissuto un identico fenomeno inspiegabile in mare nel mese di novembre 1975. Chiamatela una visione, un avvistamento o qualsiasi altra cosa che vi piace, ma da quel punto in avanti ha trovato i suoi pensieri pieni di matematica e motivi geometrici e relazioni.
http://www.solargeometry.com/origdraw.htm
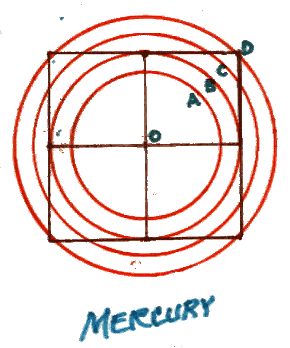
O è l’origine, il Sole; A si trova a 0.792893…Perielio di mercurio 2-0,5(√2+1); B è 1.000000….; Distanza media orbitale di mercurio, 0,5(√1+1); C è 1.207106 …, Afelio di mercurio, 0,5(√2+1); D è 1.414213 …√2 (√diametro di mercurio)
Alan ha iniziato a disegnare le immagini di poligoni geometrici e dentro di se sentiva che c’era qualcosa in questo e che aveva a che fare con il sistema solare. Questo nuovo interesse lo ha portato a studiare la scienza delle antiche civiltà. Le sue prime intuizioni sulle connessione dei suoi pensieri al sistema solare, è venuto leggendo il libro “Il segreto della Grande Piramide” di Peter Tompkins. Qui, a Alan divenne subito chiaro che, l’uomo delle antiche civiltà, era a conoscenza di alcune di quelle relazioni, sulle quali anche lui aveva lavorato e che sono apparse nella geometria delle piramidi in Messico, Cina ed Egitto.
Il lavoro che ci viene mostrato nel suo sito è estremamente interessante ed originale ed andrebbe approfondito, ma Alan credeva che molti altri prima di lui avessero avuto le stesse intuizioni sul sistema solare e che queste conoscenze sono andate perse da tanto tempo. Era la sua passione. Alan dice :
…..lascio a voi il piacere di portare questa conoscenza, nella speranza che un giorno la comprensione di queste relazioni ci porterà ad una più profonda verità del nostro universo e del nostro Creatore, che lo ha realizzato con tanta perfezione incredibile….
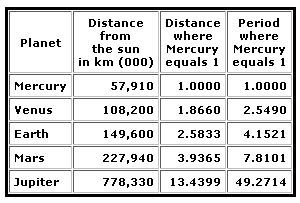
Dal tempo di Tolomeo, nel 2° secolo DC, l’uomo credeva che la Terra fosse al centro dell’universo. Nel 15° secolo, Copernico ci ha avvicinato alla verità, spostando il Sole al centro dell’universo. Successivamente Galileo, Keplero e altri, ci hanno aiutato a spostarci dalla nostra visione geocentrica dell’universo, ma alla fine del 20° secolo, la scienza esprime ancora i rapporti planetari del sistema solare grazie all’Unità Astronomica, distanza della Terra dal Sole . A parte il fatto che abitiamo la Terra, c’è qualche motivo logico per basare queste relazioni sul terzo pianeta del sistema? Siamo ancora geocentrici, e indietro, nel nostro pensiero? Prendiamo quindi un nuovo punto d’osservazione all’interno del nostro sistema solare e visualizziamo le relazioni che si ottengono quando Mercurio, viene utilizzato come misura di base per gli altri pianeti, il primo pianeta.
Quando Mercurio viene impostato ad 1, solo allora i rapporti planetari possono essere visti. Si tratta di un semplice cambiamento, ma questa nuova visione svela una incredibile visione nelle relazioni tra i pianeti. Ognuna di queste misure di distanza può essere rappresentata con un elegante motivo di interi semplici da 1 a 6 sotto radici, con moltiplicatori ed esponenti :
Mercurio = 1 = ½(√1+1) ; Mercurio all’afelio = ½ (√2+1) ; Venere = Mercurio * (½(√3 + 1)) ²
Terra = Venus¾ * (½* (√5 + 1)) ; Marte = Terra¾ * (½*(√6 + √2 )) ; Giove = Marte * (√2 + 2)
– Le geometrie solari
Le distanze di ogni pianeta dal sole possono essere descritte da un’unica rappresentazione geometrica, o geometria solare, per ogni coppia di pianeti, come mostrato di seguito.
Mercurio e il suo Afelio e Perielio
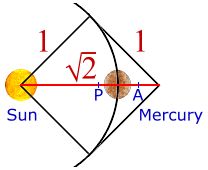
Ponendo Mercurio = 1, abbiamo che il Perielio = 2 – ½*(√2+1) = 0,792893 mentre Afelio = ½*(√2 +1) = 1,207107.
Tracciamo un cerchio per la distanza media orbitale di Mercurio, e poi costruiamo un quadrato con lati di uguale lunghezza. Il punto medio tra il raggio del cerchio e la diagonale del quadrato è all’afelio di Mercurio (A), il punto al di fuori della sua orbita. La stessa distanza verso il Sole è il perielio di Mercurio (P), il punto all’interno della sua orbita.
Mercurio e Venere
Mercurio = Venere * (½*(√3 + 1))² = 1,866025
Tracciamo un cerchio per la distanza media orbitale di Mercurio, dividiamo il cerchio in sei parti uguali, tracciamo una linea in maniera tale da formare una sezione del triangolo equilatero e successivamente disegnamo un quadrato con le linee della stessa lunghezza in maniera tale da ottenere la distanza orbitale di Venere.
Venere e Terra
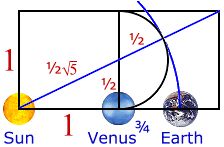
Terra = Venere¾ * ½ (√5 + 1) = 2,583306 Terra = 1.596571 * 1.618034 = 2.583306
Iniziamo con elevare a potenza ¾ la distanza orbitale di Venere, poi costruiamo la ben nota “sezione aurea” http://it.wikipedia.org/wiki/Sezione_aurea, e otteniamo la distanza media orbitale della Terra.
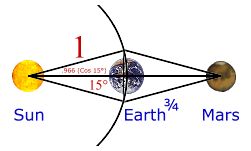
Terra – Marte
Marte = Terra ¾ * ½ (√6 + √2) = = 2.037661 * 1.931852 = 3,936458
Nota : ½ (√ 6 +√2) = 2 * Coseno 15 º = 1,931852
Inoltre : √(2 * Venere) =√(diametro di Venere) = 1,931852
Iniziamo con il tracciare un cerchio elevando nuovamente a potenza ¾, la distanza orbitale della Terra come suo raggio, dividiamo il cerchio in dodici parti uguali, tracciamo una linea per formare il triangolo isoscele della sezione e quindi disegnamo un altro triangolo isoscele sull’altro lato, utilizzando delle linee della stessa lunghezza, formiamo un rombo e otteniamo la distanza fra il Sole e Marte.
Nell’elevazione potenza a ¾ si fonda la legge del moto planetario.
A prima vista, elevare a potenza ¾ nella relazione fra Venere e la Terra e fra la Terra e Marte può sembrare strana o addirittura forzata, ma il tutto diventa chiaro una volta compresa la terza legge di Keplero del moto planetario, in cui si afferma:
“….La terza legge afferma che i quadrati dei periodi di rivoluzione dei pianeti sono proporzionali ai cubi dei semiassi maggiori delle loro orbite….”
http://it.wikipedia.org/wiki/Leggi_di_Keplero
Quindi , Distanza 3 = Periodo 2, ma se dividiamo per un quattro otteniamo, Distanza 3/4 = Periodo = 2/4 = Periodo 1/2 =√ Periodo
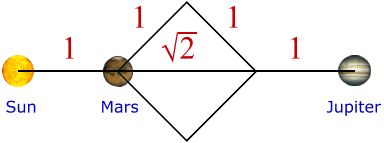
Marte – Giove
Giove = Marte * (√2 + 2) = 3.936458 * 3.414214 = 13,439908
Partiamo dalla distanza orbitale di Marte, aggiungiammo un quadrato realizzato con la distanza orbitale di Marte rivolto sulla diagonale e quindi riportiamo nuovamente la distanza orbitale di Marte e otteniamo la distanza orbitale di Giove.
—————————————————————————————————————————————————————————————————————-
La geometria solare svela alcune relazioni affascinanti tra i pianeti del nostro sistema solare. Le relazioni sembrano troppo inusuali per essere frutto del caso, ma sono l’evidenza di un disegno divino?
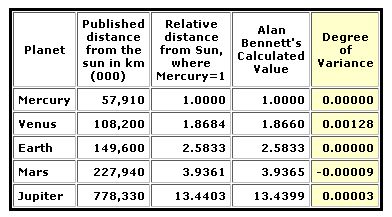
L’obiezione più significativa a queste proporzioni risiede nel semplice fatto che i rapporti planetari calcolati non sono completamente in accordo con le posizioni attuali dei pianeti. Queste differenze sono riassunte qui di seguito. Di seguito sono riportate alcune possibili spiegazioni per queste piccole variazioni osservate :
L’orbite potrebbe essersi spostate nel corso del tempo, dalla creazione del sistema solare, a causa di decadimento orbitale o l’influenza gravitazionale di altri corpi solari. Le attuali misure del sistema solare potrebbero non essere esatte. Le distanze sono espresse solo in quattro o cinque cifre significative e anche le distanze orbitali e i periodi pubblicati dalla NASA non sono del tutto accurati, come dimostrano le variazioni che risultano applicando la terza legge di Keplero ai dati.
Fonte : http://solargeometry.com/index.htm
Michele
![]()