Tutti i terremoti si verificano molto vicino alle ore 06:00 o 18:00 ora locale lunare
di Giovanni P.Gregori
IDASC (Istituto di Acustica e Sensoristica O. M. Corbino (CNR) – Roma (Italy)
IEVPC (International Earthquake and Volcano Prediction Center) – Orlando (Florida, USA)
Riassunto
Se un terremoto (EQ) deve avvenire in qualche luogo e in qualche giorno, quasi sempre accade durante uno dei due intervalli di tempo vicino alle 6:00 o alle 18:00 LLT (ora locale lunare). Questa legge si applica al ~98% dei casi. In questo studio vengono presentate le procedure e sono adattate per valutare l’esatta durata del ritardo con il 95% (o superiore) limite di affidabilità.
Introduzione
Kolvankar nel 2011 ha riportato un’analisi sistematica studiando più di 5.000 eventi sismici con una gamma di magnitudo compresa fra 2-10, basata sul catalogo sismico globale NEIC-USGS, distinguendo dei modelli separati per le diverse gamme di periodi, grandezze, profondità, latitudini e longitudini.
La traduzione del passato lavoro di Kolvankar, presentata sul nostro blog è disponibile al seguenti link :
http://daltonsminima.altervista.org/2012/02/20/sole-luna-e-terremoti-1%C2%B0-parte/
http://daltonsminima.altervista.org/2012/02/27/sole-luna-e-terremoti-2%C2%B0-parte/
Kolvankar ha trovato sempre una “legge” comune condivisa da ogni sottoinsieme di eventi, indipendenti dalla grandezza (magnitudo), la profondità, la latitudine, e il tempo, con la visualizzazione della dipendenza regolare sulla φ longitudine.
Egli considerava i seguenti angoli (se non diversamente indicato, tutti gli angoli sono in senso antiorario) :
• SEM (Sole – epicentro terremoto – Luna)
• GMT
• φ longitudine
• EMD (EQ epicentro – distanza dalla luna)
• LT l’ora locale, e
• LLT il tempo lunare locale
Le definizioni di LT e di LLT sono analoghi a vicenda, con la differenza che il punto sulla superficie della Terra con 12:00:00 LT osserva il Sole nella sua massima elevazione, mentre il punto con 12:00:00 LLT osserva la Luna nella sua massima elevazione sopra l’orizzonte.
Si noti che la figura 2, ripresa dalla carta di Kolvankar (2011) indica erroneamente (Kolvankar, comunicazione privata, 2015) il senso orario di SEM, mentre tutta la sua analisi è stata condotta su considerando SEM in senso antiorario.
Kolvankar (2011) ha mostrato che il 98% di tutti i terremoti soddisfano una relazione lineare:
(1) GMT = EMD + SEM + const
che egli mostra essere soddisfatta in diverse regioni (un esempio è mostrato in figura 2), ognuno caratterizzato da circa la stessa longitudine. Al considerando il 3° e l’ultima colonna della tabella 1 della Kolvankar (2011), si è constatato che (1) è :
(2) GMT = EMD + SEM – φ
che può essere risolto (vedi Figura 1) per ottenere:
(3) GMT + φ = LT = EMD + SEM
(4) LLT = LT – SEM = EMD
Cioè, a causa di (4), il significato fisico della relazione empirica (2) è che il 98% di tutti i terremoti occorrono molto vicino a LLT = 06 o LLT = 18 (ore di tempo locale lunare).
Questo risultato sembra fisicamente plausibile come la deformazione di marea lunare è massima a LLT = 12:00 o LLT = 0:00, ma la derivata temporale della deformazione è massima a LLT = 6:00 o LLT = 18:00, e il massimo stress sulla crosta si verifica quando il gradiente temporale è al massimo della deformazione.
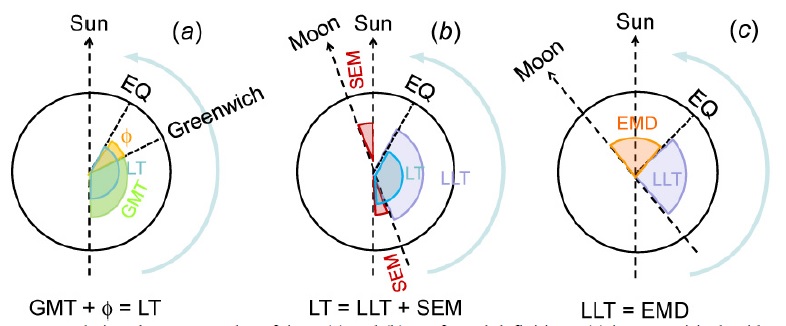 Figura 1. Alcuni relazioni tra angoli e tempo. (a) e (b) sono definizioni formali, (c) evidenza empirica. Vedere il testo.
Figura 1. Alcuni relazioni tra angoli e tempo. (a) e (b) sono definizioni formali, (c) evidenza empirica. Vedere il testo.
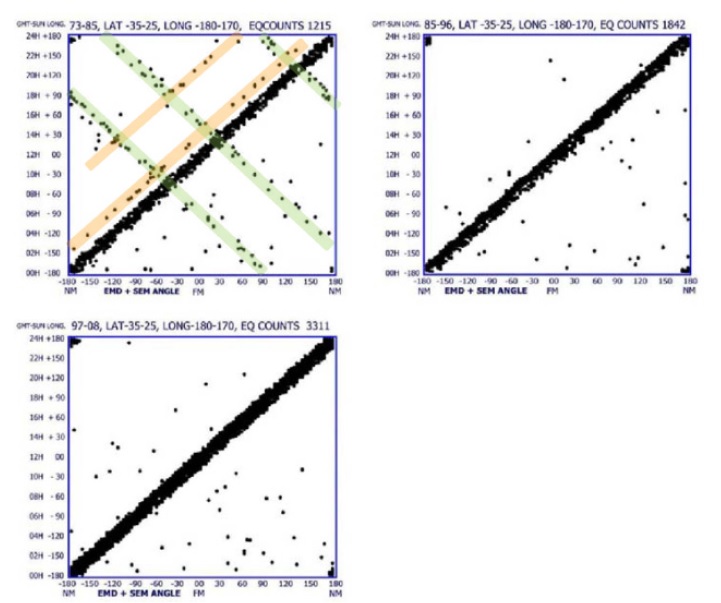
Figura 2. “Tre trame di terremoti di (EMD + SEM) Vs tempo GMT per la gamma di latitudine -35 ° a -25 ° e gamma longitudine -180 ° a -170 ° per tre periodi di tempo : 1973-1984, 1985 -1996 e 1997-2008. I terremoti occupano la stessa striscia di questi complotti e non vi sono variazioni dipendenti dal tempo “. Nota nel primo lotto [in alto a sinistra] che pochi eventi colpiscono lungo linee più o meno perpendicolare al trend principale. Vedere il testo. Figura modificato e didascalie dopo Kolvankar (2011).
…… Il risultato generale (2) ha un’applicazione più importante. Infatti, ogni volta che sarà possibile da un metodo di procedere alla segnalazione di un eventuale possibile terremoto che può essere ragionevolmente previsto colpire qualche data area, vedi (4). E quindi sarà possibile sapere che, durante le 24 ore di ogni dato giorno – e in ogni dato sito – lo shock si può verificare, con il 98% di certezza, solo durante le due finestre temporali, ciascuno di alcuni molto breve ritardo totale. Vi è tuttavia la necessità di valutare, con una barra di errore che specifica pe al limite di confidenza del 95%, la durata esatta di uno di questi due sfasamenti temporali, che sono vicini alle 06:00 o alle 18:00 LLT, rispettivamente, durante il quale un terremoto dovrebbe verificarsi. ….Questo è lo scopo della carta a breve presente, dove gli algoritmi e le procedure per la gestione dei dati sono discussi in dettaglio, anche se alcuna applicazione diretta è stata ancora attuata…
…
…..
Il lavoro prosegue con un’appendice che contiene dettagli di trigonometria sferica. Per chi volesse approfondire il lavoro ed effettuare un calcolo molto più preciso, può visionare l’analisi di Gregori pubblicata sul giornale NCGT JOURNAL Volume 3, Number 1, di marzo 2015 al seguente link : http://www.ncgt.org/newsletter.php?action=download&id=143