di agrimensore g., con la collaborazione di Fano
La “sensibilità”, in generale, è un parametro che indica come varia una grandezza a seguito della variazione di un’altra grandezza. In matematica è paragonabile alla derivata in un punto di una funzione.
Per quanto riguarda il clima, la sensibilità è spesso definita come quel parametro che ci dice di quanto aumenta la temperatura se raddoppia la concentrazione di CO2 in atmosfera. Più in dettaglio, tale parametro ne comprende due:
1) quello che ci dice di quanto aumentano le radiazioni ricevute (IR) dalla superficie all’aumentare della concentrazione della CO2 in atmosfera (forcing radiativo);
2) quello che ci dice di quanto aumenta la temperatura all’aumentare delle radiazioni che raggiungono la superficie (punto precedente).
Riassumendo, secondo l’AGWT abbiamo che: + CO2 –> + IR –> + T
In questa coppia di articoli ci occuperemo esclusivamente di analizzare il secondo punto, cioè dei problemi inerenti la valutazione dell’aumento delle temperature all’aumentare delle IR ricevute dalla superficie.
Come si è calcolato, fino ad oggi, questo parametro?
In due modi distinti:
– o con i modelli GCM (General Circulation Model)
– o col raffronto col passato.
Il tema dei modelli GCM verrà affrontato nella seconda parta, ove tratteremo dei problemi di V&V, over-fittng, training data vs. test data, variabili di input, confronto previsioni-realtà, ecc.
In questa prima parte, invece, ci occupiamo di discutere la modalità con cui si è calcolata la sensibilità climatica a partire dai dati del passato.
In sostanza, si è stabilito, con un certo margine di incertezza, che in un certo lasso di tempo (in genere di parecchi anni) si è verificato un certo forcing radiativo che ha portato ad un range di aumento delle temperature del pianeta. A questo punto, si è applicata la le legge trovata nel passato al periodo attuale.
Le stime considerate dall’IPCC per l’aumento di temperatura a fronte di un raddoppio di concentrazione di C02 vanno da 0.1C a oltre 7C, e l’IPCC assume ragionevole il range 2-4,5C. Riporto di seguito la figura, ove sono riportate anche le stime ottenute con modelli GCM, contenuta nel rapporto IPCC:
Fig.1
Come si vede dalla figura, ciò che è stato stimato non è proprio il valore parametro, quanto la probabilità (tramite la funzione densità di probabilità) che il parametro assuma un determinato valore. Già da questi studi si nota una certa discrepanza tra le conclusioni dei vari lavori, ma ne esistono altri che si differenziano ancora di più: Schwarz 2007, stima in 1.1 C +/- 0.5C (poi corretto nel 2008 in 1.9C +/- 1.1C), Shaviv ancora molto meno.
Questo grafico ci dice, tra l’altro, che un aumento minore di 1°C è improbabile per tutte le stime riportate. Ad esempio, per il lavoro di Andronova del 2001, c’è una buona probabilità che il raddoppio della CO2 inneschi un aumento della temperatura media globale di 1.5°C circa
Cosa c’è che non va in questo tipo di ragionamento?
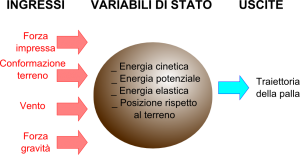
Il clima della Terra può essere esaminato dal punto di vista dell’evoluzione dei sistemi dinamici. Riassumendo la definizione di wikipedia di sistema, sappiamo che possiamo rappresentarlo come
“… una ‘scatola nera’ con ingressi ed uscite. Lo stato del sistema è descritto da un insieme di variabili, dette appunto di stato che definiscono la “situazione” in cui si trova il sistema ad un certo istante temporale. Gli ingressi agiscono sullo stato del sistema e ne modificano le caratteristiche ovvero i valori in un dato istante temporale: queste modifiche vengono registrate dalle variabili di stato. I valori delle uscite del sistema, solitamente le uniche variabili misurabili (ingressi esclusi) dipendono a loro volta dalle variabili di stato del sistema e dagli ingressi (in maniera più o meno diretta).”
Il senso delle variabili di stato è quello di costituire la memoria stessa del sistema dinamico, cioè le variabili di stato dipendono non solo dagli ingressi ad un certo istante, ma anche dal valore delle stesse variabili di stato in istanti precedenti.
Nel caso della Terra, possiamo immaginare, ad esempio, di essere in una situazione del genere:
Fig. 2a
Non è detto che i sistemi debbano essere qualcosa di particolarmente complesso. Un sistema può essere anche una semplice palla, che prendiamo a calci, su un terreno accidentato In questo caso, ad esempio, possiamo immaginare che il sistema sia di questo tipo:
Fig.2b
I sistemi si possono trovare in equiibrio oppure no, e l’equilibrio può essere stabile o instabile.
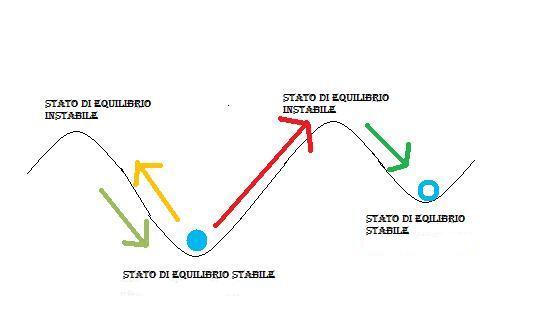
Il paragone più semplice per definire uno stato di equilibrio stabile è quello della palla in una buca: se gli si dà un calcio, la palla ritorna nella buca. A meno che il calcio non sia abbastanza forte (o tanti calcetti un appresso all’altro, prima che la palla ritorni indietro) da farla uscire dalla buca: a quel punto la palla uscirà dalla prima buca e si fermerà solo dopo aver trovato un’altra buca (nuovo stato d’equilibrio).
Viceversa, uno stato instabile può essere paragonato a quello della palla in cima ad una collina: basta un piccolo calcetto e la palla si allontanerà.
La Terra si trova, approssimativamente, in un equilibrio stabile. Ad esempio, a seguito dell’eruzione del Pinatubo, per un periodo la media delle temperature globali è diminuita a causa di quanto emesso del vulcano, ma, terminata l’eruzione, al depositarsi delle ceneri, la temperatura è tornata all’incirca come prima.
Nel corso degli anni però la Terra ha attraversato vari stati di equilibrio, passando per Younger Dryas, episodi di snowball earth, periodi caldi, ecc.
Ora, cosa accade quando uno scienziato cerca di scoprire cosa è successo migliaia, o milioni di anni fa a fronte di un forcing sul clima terrestre? Beh, se il forcing è stato abbastanza intenso, troverà che la Terra è passato in un nuovo stato di equilibrio. Viceversa, se il forcing è debole, sarà difficile isolare i suoi effetti da quelli prodotti dalla variabilità naturale.
Quindi i lavori per stimare la sensibilità riguarderanno, generalmente, casi nel passato in cui il forcing è stato così intenso che il sistema Terra ha perso il suo precedente equilibrio.
Vi sono anche delle eccezioni, come quelle che riguardano studi sul passato molto recente (es.: reazione del sistema all’eruzione del Pinatubo, risposta degli oceani, ecc.). Per il resto, i casi in cui il sistema nel corso dei millenni ha reagito ad una piccola perturbazione esterna mantenendo l’equilibrio, non sono significativi per gli studi sulla sensibilità, semplicemente perchè non lasciano una traccia chiara.
Facciamo un esempio.
La Terra (o la palla) è rappresentata dal cerchio blu, la freccia rossa indica il forcing intenso , la freccia verde la reazione del sistema (Terra o palla che sia) per ritrovare l’equilibrio.
Da questi dati, (intensità del forcing indicato dalla freccia rossa e conseguente risposta del sistema indicato dalla freccia verde) possiamo ricavarne una legge tra forcing (perturbazione) ed evoluzione del sistema (cambiamento della temperatura o spostamento della palla)? Cioè, immaginando di avere i dati su:
– quanta energia abbiamo impresso alla palla e il percorso che ha fatto o, parallelamente
– quanto energia in più ha ricevuto la Terra e la variazione di temperatura
si può ricavare una formula (o meglio, la densità di probabilità del valore di un parametro) che lega:
– l’energia impressa –> conseguente spostamento della palla? o
– l’energia ricevuta –> la conseguente variazione della temperatura?
La risposta la possiamo immaginare guardando gli effetti di perturbazioni meno intense (freccia arancione): qui la Terra (o la palla) ritorna al punto di partenza. Come si vede non c’è nessuna proporzionalità, nessuna formula, ed in particolare la traiettoria che assumerà la palla dipende dal “tipo di buca” in cui si trova. Quindi è molto complicato trovare una regola, dipende dall’evoluzione del sistema che risponde in maniera diversa in base agli altri input e allo stato in cui si trova.
Com’è possibile ciò?
Questo avviene quando sul sistema agiscono dei feed-back negativi (controreazioni) che costringono il sistema al suo punto di equilibrio.
Nel caso della palla, il feed-back è la sua stessa posizione rispetto al terreno, a fronte della traittoria. Insieme alla gravità, determina il riposizionamento alla posizione iniziale, se l’intensità del calcio non è troppo forte.
Nel caso del clima, posso immaginare un feed-back dato dal ciclo idrico, cioè dal vapor acqueo. Ora se il vapor acqueo si trasforma in:
– “nubi medio-basse”, allora avremo un feed-back negativo per aumento dell’albedo
– “gas in atmosfera”, allora avremmo un feed-back positivo perché aumenta l’effetto serra.
Poiché la Terra si è dimostrata abbastanza stabile, almeno nelle ultime migliaia di anni, appare ragionevole che si verifichi la prima ipotesi, ma si può fare un’ulteriore congettura: può darsi che il trasformarsi o meno del vapore in nube dipenda da un fattore esterno, come ad esempio i GCR (cfr. esperimento Cloud al Cern). Ultimamente se n’è parlato anche su CM, a proposito di un nuovo studio http://www.climatemonitor.it/?p=14202
Nell’AGWT, invece vengono descritti molti feed-back positivi, il più importante dei quali è il seguente:
+ CO2 –> + temp –> + CO2 –> +temp –> + CO2 –>…
Il feed-back positivo è proprio di un sistema in uno stato instabile: qualsiasi perturbazione, anche casuale e minima, aumenti il livello di CO2 o temperatura, conduce ad un incremento di ambedue le grandezze fino a trovare un nuovo equilibrio. In questo caso, è ancora più difficile trovare un legame tra input e output, giacchè uno amplifica l’altro.
Ma il problema di fondo è che anche nel caso di un sistema semplice, come una palla presa a calci su un terreno sconnesso, è sostanzialmente impossibile, soltanto con l’osservazioni di qualche esperienza precedente, trovare la legge universale che regola il processo. Cioè, non c’è una formula che permette di ricavare a fronte di un calcio (rasoterra) la traiettoria della palla: bisogna conoscere il “terreno” in ogni suo punto, altrimenti non ci si riesce.
E’ come se volessimo stimare il risultato finale di una partita, basandoci sulla serie storica degli incontri tra le due avversarie. Anche se i giocatori fossero sempre gli stessi, quanto può essere efficace tale strategia, senza conoscere la forma fisica degli atleti, le motivazioni, ecc.? Persino all’interno di un periodo di tempo breve, due squadre che si affrontano ottengono risultati completamente diversi tra “andata e “ritorno”, non tanto per l’alea, quanto per il diverso rendimento dei giocatori (è diverso il loro “stato”).
In sostanza, a livello teorico è lecito provare a trovare una somiglianza (likelihood) di comportamento delle variabili di stato in due diversi istanti basandosi sui dati passati, ma è necessario avere la conoscenza più completa possibile del sistema.
Riportato alla sensibilità climatica, questo significa che bisogna conoscere come funziona nella sua interezza il sistema Terra per provare a stimare tale parametro. Presumibilmente, non basta confrontarsi col passato, è necessario comprendere ogni meccanismo che possa influenzare il clima.
Questo non significa che gli scienziati non abbiano fatto un buon lavoro, o, peggio siano in malafede. Semplicemente, i loro risultati non vanno considerati come definitivi, ma qualcosa da dover comprovare tramite una fase sperimentale, che però è estremamente difficile perchè non abbiamo a disposizione un altro pianeta da laboratorio.
E quindi?
N.Scafetta (Duke University) scrive così:
http://www.fel.duke.edu/~scafetta/pdf/21mo-secolo.pdf
Secondo l’IPCC se la concentrazione atmosferica di CO2 raddoppia la temperatura media del pianeta potrebbe aumentare tra 1,5 e 4,5 oC. La distribuzione della sensibilità climatica al CO2 (…) varia entro un intervallo perfino più largo di 1,5 e 4,5 oC. Se gas serra come la CO2 sono la maggiore causa del riscaldamento globale, una sensibilità climatica alla CO2 con un errore minimo del 50% non può che suscitare forti perplessità sulla robustezza delle interpretazioni dei cambiamenti climatici dell’IPCC. Questo errore macroscopico è dovuto al fatto che non si sanno modellare bene i principali meccanismi climatici di feedback, cioè il vapore acqueo e le nuvole.
Inoltre, come si vede in fig.1, per ogni studio i valori più probabili non sono nemmeno vicini ai valori medi (max di densità rispetto al valore segnato dal pallino). Prendendo per buoni i lavori dei vari scienziati riportati e anche non considerando i lavori degli scienziati considerati scettici, diventa davvero difficile, a fronte di risultati così variabili, trarne delle indicazioni.
Riassumendo, benché non proprio impossibile in via teorica, in pratica, dal confronto col passato, appare davvero complicato trovare una legge affidabile che lega il forcing radiativo con i suoi effetti sulla temperatura in un sistema così complesso come la Terra. Se si vuole ottenere un ragionevole livello confidenza della stima prodotta, bisognerebbe pensare ad un esperimento (attività sperimentale), che possa comprovarla.
In assenza di questo, si è trovata un’altra possibilità: l’uso di modelli GCM che cercano di simulare il sistema Terra, o meglio individuare dei valori statistici affidabili di alcune grandezze fisiche proprie del clima.
Ma di questo parleremo nella seconda parte.