E’ un pò che ci penso e mi pare che anche qui nel blog si stiano esprimendo per lo più opinioni personali …

La domanda che pongo e’ : per far aumentare i ghiacci polari (le banchise, intendo) conviene molto freddo assai concentrato (Vortice polare chiuso) oppure e’ meglio che il freddo , seppur di minore intensità, sia sparso su di un’area superiore ?

L’unico modo per rispondere, a mio avviso e’ fare due conti .

E come al solito ve li propongo sulla carta di formaggio.  Mi scuso in anticipo se ho dovuto usare un pelo di calcolo integrale ma… chi non lo conosce dovrà fidarsi e chi lo conosce, per favore controlli i conti….

Cominciamo con il modelino :

• Mettiamo dell’acqua a zero gradi (Mare)
• Mettiamoci sopra del ghiaccio (che poi andrà a tendere a zero ma per ora mettiamocelo)
• Mettiamo sopra il ghiaccio dell’aria fredda.

Usando formule ottocentesche si trova che il “calore” fluirà verso l’esterno ostacolato dalla “Resistenza termica” del ghiaccio. Più e’ spesso il ghiaccio e meno calore fluisce, più e’ grande la superficie e maggior calore fluisce.

Altre formule ottocentesche ci dicono che per far “gelare” l’acqua occorre sottrargli una certa quantità di calore .

Nel primo foglio vedete i conti che portano a ricavare la “velocità di congelamento” di una colonna d’acqua :

Come si vede la velocità di congelamento e’ inversamente proporzionale allo spessore deh ghiaccio. Ciò significa che lo spessore aumenta nel tempo con legge LOGARITMICA (quindi pian piano la formazione rallenta, senza per altro fermarsi mai… vedi grafico del logaritmo preso da wikipedia , la parte che ci interessa e’, ovviamente, quella positiva del grafico in quanto ghiaccio con spessore negativo non ha molto senso fisico… )

Ora però voglio essere più cattivo. Supponiamo che la temperatura sia differente man mano che ci allontaniamo dal centro del cilindro (ma resti costante lungo la circonferenza) .

Dovremo procedere ad una integrazione “a cipolla” considerando cilindretti infinitesimi.

Seguite il ragionamento riportato nel foglio seguente (cliccateci sopra se non vedete bene)… oppure fidatevi (male!)

Miracolosamente risulta che la dipendenza dello spessore  di ciascun cilindretto dal tempo e’ sempre logaritmica ma dipende anche dal “differenziale di temperatura” che si verifica localmente.

A questo punto facciamo il conto che ci interessa: il volume totale.  Per vostra delizia devo integrare di nuovo (e vi confesso che la probabilità che, su tre integrazioni, abbia fatto un errore e’ prossima all’unità) supponendo una distribuzione di temperatura sulla nostra calotta simulata. Per non farmi problemi ulteriori suppongo che vada da 0°C ai bordi del noostro cilindrone (cioè, più in la non si forma ghiaccio) a T0 del centro (la nostra temperatura del Polo Nord).

Seguite ( e chi sa controlli i conti, mi raccomando) e troverete che…

Il Volume totale di ghiaccio formato e’ sempre logaritmico nel tempo ma solo DIRETTAMENTE PROPORZIONALE ALLA TEMPERATURA PIU’ FREDDA mentre e’ PROPORZIONALE AL QUADRATO ( e dico quadrato!!!) della distanza a cui la temperatura scende a zero gradi   (Appalusi)

(Nell’ultima formula l’R al cubo al numeratore dovrebbe essere un R’, e quindi si semplifica con il denominatore… Visto che bravo? Mi sono trovato da solo un errore! Solo che oltre ad essere distratto sono anche pigro e non ho voglia di scannerizzare di nuovo il foglio… Inoltre la T va inseita con valore positivo… intesa come differenza tra zero e la T negativa)

Ho provato a plottare l’andamento della funzione (ovviamewnte solo per vedere come si comporta, senza pretesa di mettere dei valori reali … questo lo lascio a chi ha i numeri per farlo) ed ecco il risultato :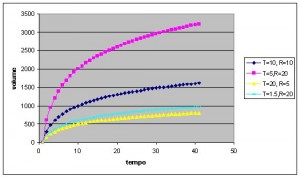

La traccia blu e’ stata relizzata con T=10 e R=10.

Poi ho dimezzato T e raddoppiato R (Traccia viola) e viceversa(Traccia gialla). La differenza e’ impressionante. Per avere più o meno lo stesso risultato della traccia gialla , con R=20  sono dovuto scendere a una delta T ridicolo di 1.5 (traccia azzurra)!

Chiarmente il tutto vale con le approssimazioni del caso… ad es. non e’ vero che tutta l’acqua sia li pronta a congelarsi quando siamo sul bordo della banchisa, non ho tenuto conto della conducibilità “trasversale” nel ghiaccio, non ho la minima idea di come si abbassino le temperature se il vortice si “spappola” ecc. ecc. Però sarei propenso a sbilanciarmi sul fatto che e’ molto meglio un vortice polare “tiepidino e spappolato” di uno freddissimo ma “chiuso a riccio”

Ma penso che un’idea ve la possiate essere fatta…

Luca Nitopi